개념 기사 기사 작성법

내가 아는 수학개념을 쉽게 설명해주세요!

기사 작성법

좋은 기사를 쓰려면 어떻게 해야 할까요?

매스포터 여러분 안녕하세요!
'기사'라고 하니 거창해 보이지만, 기사는 형태가 다른 하나의 글이랍니다. 기사라고 반드시 신문에서 보는 기사 형태일 필요는 없습니다. 수학동아의 다양한 기사를 보고 자유로운 형식으로 써주세요! 본격적으로 기사를 쓰기 앞서 좋은 기사를 쓰기 위한 몇 가지 '꿀팁'을 알려 드릴게요. 이것만 지켜도 훌륭한 기사를 쓸 수 있답니다!

01 제목 정하기

기사를 볼 때 가장 먼저 보는 게 무엇인가요? 바로 제목입니다. 아무리 잘 쓴 기사라도 제목이 재미없으면 눈길이 안 가기 마련입니다. 기사의 제목은 기사의 주제를 담고 있으면서도 사람들의 흥미를 끌 수 있어야 합니다.
02 육하원칙 지키기

도형의 기본 요소가 점, 선, 면인 것처럼 문장의 기본 요소는 '육하원칙(언제, 누가, 어디서, 무엇을, 어떻게, 왜)'입니다. 육하원칙을 잘 지킨 문장은 명확하고 많은 정보를 담고 있기 때문에 이해하기가 쉽습니다.
03 띄어쓰기와 맞춤법 지키기

기사의 목적은 새로운 정보를 정확하게 전달하는 것입니다. 그런데 기사에 띄어쓰기나 맞춤법이 잘못돼 있으면 신뢰하기 어렵겠죠? 기사를 다 쓰고 잘못 쓴 단어나 문장은 없는지 한 번 더 확인해주세요.
04 문장은 짧게, 다양한 단어 이용하기

한 번에 읽기 편하도록 문장은 짧게 써주세요. 문장이 길어지면 주어와 서술어가 맞지 않거나, 같은 말을 반복하는 등의 실수를 하기 쉬워요. 문장을 줄이고 싶으면 '굉장히', '매우'와 같은 미사여구나 '그런데', '따라서'와 같은 접속사 중 불필요한 표현을 빼주세요. 또 한 문장에서 같은 단어가 되풀이되지 않게 다양한 단어를 이용해보세요. 글이 훨씬 풍성해 질 거예요.
05 사진 또는 그림 설명하기

기사 내용과 관련 있는 사진과 그림에 대한 설명을 꼭 달아주세요! 기사의 내용을 이해하는 데 큰 도움이 된답니다. 이때 본인이 직접 찍은 사진만 사용해 주세요. 포털 사이트에서 허락없이 가져오는 사진이나 그림은 저작권에 문제가 될 수 있습니다. 저작권에 문제가 없는 사진일 경우 꼭 출처를 밝혀주세요!
Plus + 재미있는 퀴즈 내기

매스포터에서는 기사의 마지막에 기사 내용과 관련 있는 퀴즈를 내야 합니다. 퀴즈를 통해 기사를 읽는 사람들이 내용을 한층 더 깊게 이해할 수 있을 거예요!

위의 사항을 제대로 지키지 않은 기사는 홈페이지에 보이지 않을 수 있으니, 꼭 ‘기사작성법’을 숙지하고 기사를 작성해주세요

[개념 기사] 초입방체란?

원파 2020.07.19 11:05

페이스북 트위터 카카오톡 카카오스토리 네이버블로그 네이버밴드

안녕하세요? 오늘은 4차원 세계에 사는 초입방체를 인터뷰해보려고 합니다. 우선, 4차원에 대해 말씀드리겠습니다.

차원에 대해 생각해보면, 0차원은 점, 1차원은 직선, 2차원은 정사각형, 3차원은 정육면체가 항상 기본꼴이 되고, 이들에서 확장되어 더 다양한 도형들이 만들어집니다. 우리보다 낮은 차원인 0, 1, 2 차원들은 있는데, 4차원도 있지 않을까요? 여러분, 이제 제 말에 집중해주세요. 눈을 감고, 머릿속에 3차원 정육면체의 형태를 떠올려보세요. 어떤가요?

(출처 : 위키피디아)

이런 것, 떠올리지 않으셨나요? 자, 그럼 이번에는 4차원의 기본형 초입방체의 형태를 떠올려봅시다. 어떤 그림이 떠오르셨나요?

많은 분들은 정육면체는 잘 떠오르셨을 겁니다. 그런데, 4차원이요? 4차원은 과연 어떻게 생겼을까요?

조금 더 설명드리고 싶지만, 초입방체가 충분히 알려줄 수 있을 것 같네요. 그럼, 지금부터 초입방체와의 인터뷰를 시작합니다!

소피 : 안녕하세요? 자기소개 부탁드립니다.

초입방체(이하 초방) : 아,안녕하세요..? 전 초입방체입니다.

소피 : 초입방체는 4차원의 기본꼴이라고 알고 있습니다. 4차원은 어떻게 생겼나요?

초방 : 3차원 세계에 사는 여러분께는 이해하기 너무나도 어려울 거에요.

소피 : 그럼, 조금 맛만이라도 보고 싶어요. 어떻게 하면 이해하기 조금이나마 쉬울까요?

초방 : 그렇다면, 차원들의 규칙을 살펴볼게요! 0차원인 점은 모든 차원의 근본이 됩니다.

소피 : 1차원인 직선은 점을 한 방향으로 길게 잡아당긴, 혹은 여러 개를 배열한 형태로 볼 수 있겠죠?

초방 : 맞아요! 그렇다면, 2차원, 3차원도 아시나요?

소피 : 2차원인 면은 직선을, 점을 잡아당긴 방향과 직교하는 방향으로 직선을 다시 길게 잡아당긴 형태가 되죠. 그리고, 3차원인 입체는 면을 이번에는 두 직교하는 방향과 모두 직교하게, 즉 '위'로 잡아당겨 만들 수 있을거에요.

초방 : 잘 아시는걸요? 그럼, 제가 표로 정리해볼게요~

0차원 (점)	기본형인 점.
1차원 (직선)	점을 한 방향으로 잡아당김.
2차원 (면)	직선을 위의 '한 방향'과 직교하는 방향으로 잡아당김.
3차원 (입체)	면을 위 두 방향과 모두 직교하게 '위'로 잡아당김.

소피 : 글씨로만 보니까 조금 헷갈려요. 사진 같은 자료는 없나요?

초방 : 보여드릴게요. 아래 그림이에요. 여기서는 3차원까지, 그리고 X, Y, Z 축만 보면 됩니다.

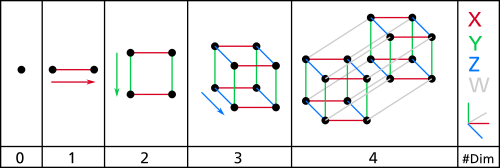
(출처 : 위키피디아)

소피 : 그림으로 보니 이해가 쉽네요. 정리해주신 표가 4차원과 어떤 관계가 있죠? 이건 저희가 이미 알고 있는 0, 1, 2, 3차원에 대한 얘기 뿐이잖아요.

초방 : 이제 얘기하려고 했어요~ 4차원을 알아보려면 더 낮은 차원에 대해 잘 알아야 한다구요.

소피 : 4차원을 알아보는데 더 낮은 차원이 왜 필요한 것인가요?

초방 : 차원은 규칙성이 있어요. 아는 내용을 바탕으로 다음 차원에 대해 예상해 볼 수 있죠.

소피 : 그렇다면, 1차이 나는 차원끼리의 관계를 알아봐야 겠는걸요?

초방 : 맞아요! (0, 1), (1, 2), (2, 3) 차원의 쌍들끼리 서로의 관계를 알면, 규칙성을 찾아 (3, 4) 차원의 쌍의 관계를 알아낼 수 있고, 따라서 4차원에 대해 예측해볼수 있답니다! 그럼, 지금부터 규칙을 알아볼게요. 1차원은 0차원을 한 방향으로 잡아당깁니다. 2차원은 1차원을 0차원을 잡아당긴 방향과 직교하는 방향으로 잡아당기고요. 3차원은 2차원을 0, 1차원을 잡아당긴 방향과 모두 직교하는 방향으로 잡아당깁니다. 그렇다면 1 차이나는 차원들 사이의 관계를 이번에도 표로 정리해볼게요.

0, 1차원	0차원을 한 방향(A)로 잡아당겨 1차원을 만듦.
1, 2차원	1차원을 A와 직교하는 방향 B로 잡아당겨 2차원을 만듦.
2, 3차원	2차원을 A, B와 모두 직교하는 방향 C로 잡아당겨 3차원을 만듦.

여기서 A는 평면의 한 방향이 되고, B는 이 방향과 직교하는 동일 평면 상의 방향이 됩니다. 또, C는 A, B가 존재하는 평면을 벗어나 '입체'라는 공간에 있습니다. 바로 우리가 '위', 혹은 '아래' 라고 표현하는 '높이' 에 존재하죠.

소피 : 그렇다면...? 4차원은 3차원 정육면체를 A, B, C와 모두 직교하는 새로운 방향 D로 잡아당겨야 하겠어요.

초방 : 정확해요!!! 그러나 3차원의 여러분들은 4차원에만 존재하는 방향 D를 알 수 없죠.

소피 : 그렇기 때문에 저희가 4차원을 이해하기 힘든 거군요. 이 D로 잡아당긴 형태는 어떻게 되나요?

초방 : 3차원의 여러분은 시야로 평면을 봅니다. 세상이 담긴 평면 말이죠. 어찌됬건 여러분의 눈은 바라보는 곳을 평면으로밖에 볼 수 없습니다.

소피 : 아닌데요? 저흰 입체를 봐요! 저희가 평면을 보면 입체인 세상에서 어떻게 살겠어요?

초방 : 이런게 바로 차원의 신비이자 가장 이해하기 힘든 점입니다. 예를 들어볼게요. 당신은 2차원에 사는 정삼각형입니다. 당신은 눈으로 2차원을 볼 수 있겠어요?

소피 : 음... 제가 2차원을 볼 수 있다면 전 2차원 세계의 '위' 에서 관찰하고 있게 되므로 전 2차원에 사는 게 아닌거겠네요...

초방 : 그래요. 그래서 모순되죠. 그렇다면 2차원인 당신은 무엇을 보겠어요?

소피 : 음, 1차원의 직선을 눈으로 보지 않을까요?

초방 : 맞아요. 그럼 3차원인 당신은 무엇을 보겠어요?

소피 : 이, 이차원을 보겠죠...

초방 : 어려워할 것 없어요! 차원은 단지 아는 것에서 규칙을 찾아내 다음 차원을 유추해내는 것 뿐이거든요!

소피 : 이번에도 그림 하나만 보여주시면 안될까요? 점점 4차원으로 올라갈수록 헷갈려지네요..

초방 : 그래요. 이번 그림은 아래와 같아요.

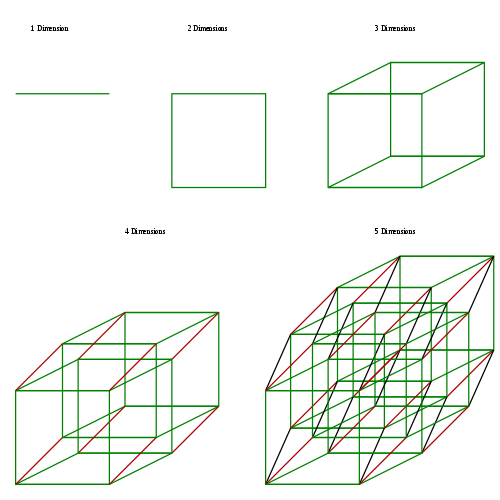
(출처 : 위키피디아)

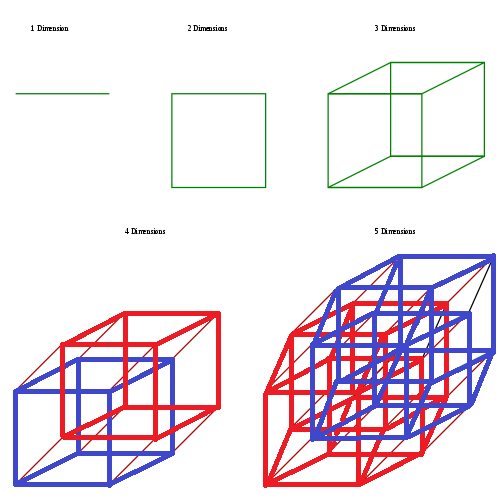
소피 : 아까 그림과 비슷하네요~! 1차원, 2차원, 3차원 사이의 관계를 자세히 알 수 있고, 4차원은 물론 5차원도 그려져 있군요!

초방 : 맞습니다. 4차원 그림을 자세히 보면, 정육면체(초록)을 평행하게(주황) 잡아당겨서 만든 모습을 보실 수 있습니다.

소피 : 아... 보이기도, 안보이기도 하네요. 좀 더 자세히 보여주세요.

초방 : 아래는 편집한 사진이에요. 출처는 동일하구요.

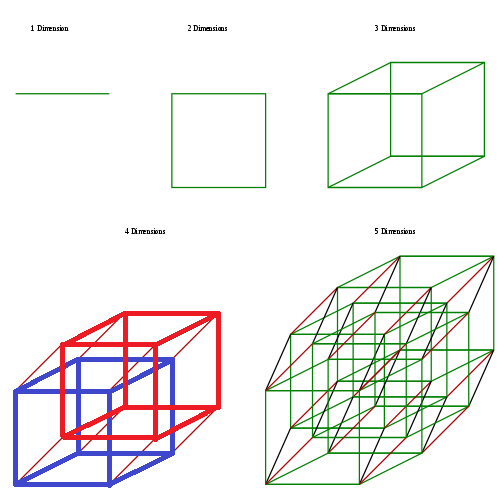
소피 : 아하! 4차원에서는 저렇게 정육면체끼리 겹칠 수 있군요! 5차원도 저렇게 그려주세요.

초방 : ㅂㄷㅂㄷ...... 힘들다고요!!!

소피 : 앗...

초방 : 게다가 처음에 4차원 알아본다면서요?! 5차원은 왜 필요하신거죠?

소피 : 지,진정하세요...

초방 : 알겠어요... 자, 그래서, 각 차원으로 이동할 때마다 이전 차원을 쭈욱 잡아당긴다고 생각하면 이해하기 쉬워요.

소피 : 그렇군요.

초방 : 이처럼 정사각형이 3차원 공간으로 이동하면서 남기는 흔적이 정육면체가 되는 것처럼 정육면체가 4차원 공간으로 이동하면서 남기는 흔적을 4차원 도형으로 생각할 수 있고, 이 도형을 테서랙트(Tesseract)라고 하며 더 넓은 의미에서 초입방체(hypercube)라고 부릅니다.

소피 : 이제 초방님의 형태를 잘 알 수 있을 것 같아요!

초방 : 제 형태를 잘 알 수 있다...

소피 : 큼큼. 그럼, 이것으로 이번 인터뷰를 마치겠습니다. 초방님, 인터뷰 참여해주셔서 감사합니다.

---------------------

오늘의 퀴즈~!

4차원 공간의 기본꼴이 되는 도형의 이름은 무엇일까요?

(1) 직선

(2) 정육면체

(3) 정육각뿔

(4) 초입방체

(5) 정사각형

태그

#차원 #4차원 #초입방체

A PHP Error was encountered

Severity: Warning

Message: Undefined variable $tag_news_list

Filename: inc/article_view.php

Line Number: 90

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/article_view.php
Line: 90
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Article.php
Line: 221
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: Cannot modify header information - headers already sent by (output started at /volume1/web/PhpstormProjects/www_polymath_co_kr/system/core/Exceptions.php:271)

Filename: core/Common.php

Line Number: 570

Backtrace:

An uncaught Exception was encountered

Type: TypeError

Message: count(): Argument #1 ($value) must be of type Countable|array, null given

Filename: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/article_view.php

Line Number: 90

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Article.php
Line: 221
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once