(출처는 뒷부분에 따로 표시)
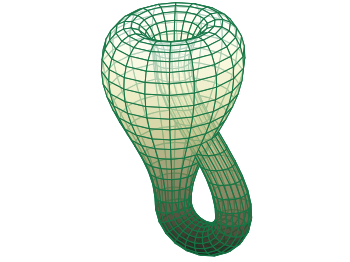
클라인 병이란, 면이 하나로 연결되어 있는 경계선이 없는 4차원의 도형입니다. 바깥쪽 면과 안쪽 면이 구분되지 않기 때문에 이 병은 3차원 공간에서 만들기 위해서는 옆쪽에 구멍을 뚫어야 해 경계선이 생겨버리죠. 결국 클라인 병은 4차원에서 존재해야지만 자연스러운 도형이라 할 수 있습니다.
이 클라인 병의 면을 훑어 봅시다.
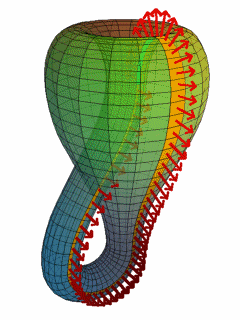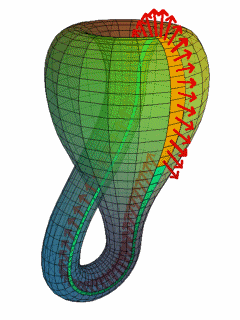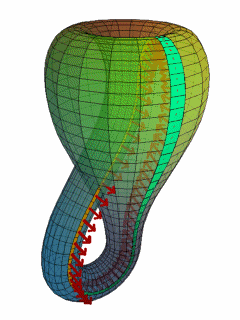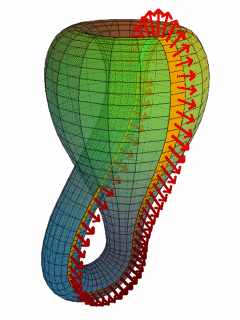(출처는 나중에)
위의 gif와 같이 면을 훑다 보면 안쪽에 들어갔다가 바깥쪽 면으로 나와서 다시 안쪽으로 들어오는 것을 보실 수가 있습니다.
이는 3차원의 도형 중 하나인 뫼비우스 띠와 매우 유사한 형태입니다.
(https://www.pinterest.co.kr/pin/444167581970330288/)
뫼비우스 띠는 앞면과 뒷면이 연결된 단 하나의 면으로 이루어져 있으며, 모서리 수도 보면 오직 1개라는 것을 알 수 있습니다.
다각형처럼 하나의 면을 이루어진 도형은 3차원의 공간 속에 있어도 2차원이라 하지만, 이 뫼비우스의 띠는 특별하게도 하나의 면이지만 3차원 도형이라 할 수 있습니다.
마찬가지로 클라인 병도 하나의 공간으로 이루어져 있지만, 4차원의 도형이라는 것입니다.
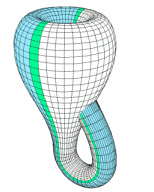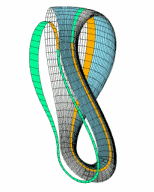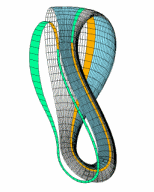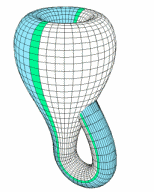
마지막으로 하나 신기한 점은 클라인 병을 2개로 잘랐을 때에 이루어집니다.
(마찬가지로 출처는 나중에)
위와 같이 단면이 뫼비우스 띠로 되어 있음을 알 수 있습니다.
※퀴즈
클라인 병은 공간은 하나지만 3차원에서는 표현할 수 없는 이유는?
(위의 것들 출처:
A PHP Error was encountered
Severity: Notice
Message: Undefined variable: tag_news_list
Filename: inc/article_view.php
Line Number: 90
Backtrace:
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/article_view.php
Line: 90
Function: _error_handler
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Article.php
Line: 221
Function: view
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once
A PHP Error was encountered
Severity: Warning
Message: count(): Parameter must be an array or an object that implements Countable
Filename: inc/article_view.php
Line Number: 90
Backtrace:
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/article_view.php
Line: 90
Function: _error_handler
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Article.php
Line: 221
Function: view
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once
이 주제는 흥미로우면서도 아리송해서 더 매력있어요.
아마 독자 여러분도 이 글을 읽고 나면 여러가지 궁금증이 생길 거예요. 글을 쓴 '전자기역학' 기자도 마찬가지일 거고요.
클라인병은 3차원 입체도형처럼 보이지만 4차원에서만 존재한다니?
구멍을 뚫고 안 뚫고에 따라 도형의 차원이 달라지는 이유는?
뫼비우스의 띠는 그래서 2차원 도형인가, 3차원 도형인가? 등이요.
기사를 읽거나 쓰고 나서 뭔가 알 것 같으면서도 정확히 설명하기는 어려운 느낌이 있다면 관련 자료를 꼭 찾아보길 바라요.
http://blog.naver.com/PostView.nhn?blogId=forfriend5&logNo=220478991707
https://www.youtube.com/watch?v=A9AS_jZyZfQ
저도 잠깐 찾아봤는데 클라인 병이 어떻게 만들어지는지도 훨씬 명확히 알게 됐고, 기사에 나온 표현의 의미도 이해하게 됐어요.
이렇게 궁금했던 부분을 나름대로 정리해본다면 앞으로 기사 내용도 풍부해지고 문장도 정확하게 구사할 수 있을 거예요!
좋아요
17
유익해요
4
웃겨요
0
신기해요
1
어려워요
0
-
article.reply.showForm('2507'); $('#is_clear').parent().hide()">댓글 작성하기 좋아요0 댓글수1
4차원의 뫼비우스의 띠라니 정말 흥미롭네요.
아마 저것도 4차원이 3차원으로 투영되어 보이는 걸까요?
4차원은 정말 신비로운 것 같아요.
그러면 저 뫼비우스의 띠를 만들기 위해서, 다른 하나의 축을 어떻게 해야 할까요?
그러니까, 공간의 세 축이 x,y,z축이고, 4차원의 축이 w축이라고 하면, w축을 어떻게 변환시켜야 저 모양을 만들 수 있을까요?
시간의 축으로 저걸 만들 수 있을까요?
어쨌든 좋아요 박고 갑니다!
-
기본적인 차원의 원리에 따르면, 시간 축과 공간 축 하나씩은 90도 회전을 해 바뀔 수 있습니다. 이건 당연한 사실이죠. 그러니 4차원에서는 시간과 공간이 서로 연관성이 많아서, 공간축을 변형시키면 시간 축이 된다는 것입니다.
하지만 다른 의미로, 수학에서의 차원이랑 공간 축만 말하는 것이기도 합니다. 클라인 병은 기하학적 접근이 필요하니, 수학적인 차원으로 보는 것이 더 자연스러우지 않을깝쇼좋아요0
그렇다면 클라인병에 물을 넣으면 어떻게 되나요?
좋아요 누르고 갑니다.
-
내부랑 외부랑 연결되어 있어서 아마 4차원에선 안 들어갈 거 같아요
좋아요0 -
물이 병 안에 갇힐 것 같은데요?
좋아요0 -
만약 3차원에서 구멍을 뚫어서 가짜 클라인병을 만들면 당연히 물이 차겠지만, 실제 4차원 클라인병이라면 면이 하나로 연결되 있어서 물이 차지 않습니다.
좋아요0 -
안들어가지 않을까요? 물을 넣자마자 다시 나올 거 같습니다
좋아요0
정말 신기하고 흥미롭네요! 클라인 병에 대해 잘 몰랐는데, 알게 되어서 좋았어요. 클라인 병의 단면이 뫼비우스의 띠라는 것도 놀랍네요.
좀 헷갈리네요;; 흥미로운 기사였습니다
