자유 기사 기사 작성법

일상생활 속 수학을 찾아 보세요!

기사 작성법

좋은 기사를 쓰려면 어떻게 해야 할까요?

매스포터 여러분 안녕하세요!
'기사'라고 하니 거창해 보이지만, 기사는 형태가 다른 하나의 글이랍니다. 기사라고 반드시 신문에서 보는 기사 형태일 필요는 없습니다. 수학동아의 다양한 기사를 보고 자유로운 형식으로 써주세요! 본격적으로 기사를 쓰기 앞서 좋은 기사를 쓰기 위한 몇 가지 '꿀팁'을 알려 드릴게요. 이것만 지켜도 훌륭한 기사를 쓸 수 있답니다!

01 제목 정하기

기사를 볼 때 가장 먼저 보는 게 무엇인가요? 바로 제목입니다. 아무리 잘 쓴 기사라도 제목이 재미없으면 눈길이 안 가기 마련입니다. 기사의 제목은 기사의 주제를 담고 있으면서도 사람들의 흥미를 끌 수 있어야 합니다.
02 육하원칙 지키기

도형의 기본 요소가 점, 선, 면인 것처럼 문장의 기본 요소는 '육하원칙(언제, 누가, 어디서, 무엇을, 어떻게, 왜)'입니다. 육하원칙을 잘 지킨 문장은 명확하고 많은 정보를 담고 있기 때문에 이해하기가 쉽습니다.
03 띄어쓰기와 맞춤법 지키기

기사의 목적은 새로운 정보를 정확하게 전달하는 것입니다. 그런데 기사에 띄어쓰기나 맞춤법이 잘못돼 있으면 신뢰하기 어렵겠죠? 기사를 다 쓰고 잘못 쓴 단어나 문장은 없는지 한 번 더 확인해주세요.
04 문장은 짧게, 다양한 단어 이용하기

한 번에 읽기 편하도록 문장은 짧게 써주세요. 문장이 길어지면 주어와 서술어가 맞지 않거나, 같은 말을 반복하는 등의 실수를 하기 쉬워요. 문장을 줄이고 싶으면 '굉장히', '매우'와 같은 미사여구나 '그런데', '따라서'와 같은 접속사 중 불필요한 표현을 빼주세요. 또 한 문장에서 같은 단어가 되풀이되지 않게 다양한 단어를 이용해보세요. 글이 훨씬 풍성해 질 거예요.
05 사진 또는 그림 설명하기

기사 내용과 관련 있는 사진과 그림에 대한 설명을 꼭 달아주세요! 기사의 내용을 이해하는 데 큰 도움이 된답니다. 이때 본인이 직접 찍은 사진만 사용해 주세요. 포털 사이트에서 허락없이 가져오는 사진이나 그림은 저작권에 문제가 될 수 있습니다. 저작권에 문제가 없는 사진일 경우 꼭 출처를 밝혀주세요!
Plus + 재미있는 퀴즈 내기

매스포터에서는 기사의 마지막에 기사 내용과 관련 있는 퀴즈를 내야 합니다. 퀴즈를 통해 기사를 읽는 사람들이 내용을 한층 더 깊게 이해할 수 있을 거예요!

위의 사항을 제대로 지키지 않은 기사는 홈페이지에 보이지 않을 수 있으니, 꼭 ‘기사작성법’을 숙지하고 기사를 작성해주세요

[자유 기사] 우리가 그냥 지나친, 작은 보드게임 도블 속 재미있는 수학원리

니유토갬 2020.06.23 21:49

페이스북 트위터 카카오톡 카카오스토리 네이버블로그 네이버밴드

요즘 코로나-19로 인해, 많은 사람들이 집에서 정말 힘들게 살고 있는데요, 이럴 때 가끔 아이들은 집에 있는 물건을 보기 시작합니다.

놀 만한 물건을 찾다보면, 보드게임이 나오고는 합니다.

저 또한, 코로나-19 초반에는 동생과 보드게임을 해주면서 놀아주었습니다.

폴리매스에서도 이러한 이벤트를 해서, 저도 당첨된 것을 보고, 엄청 신났었죠.

따라서, 저는 이 주제로 기사를 쓰기로 했습니다.

보드게임의 기초에 대해 먼저 알아보자면, 보드게임은 도구들, 즉, 말판, 보드판, 주사위 등을 이용하여, 재미있게 즐기는 게임입니다.

원래는, 게임으로 부르다가, 컴퓨터게임과는 완전히 다른 게임이라고 생각되어, 보드게임이라고 칭하게 되었습니다.

크게는 유로게임, 테마게임, 워게임, 추상전략게임으로 구별하는데, 모노폴리 같은 게임은 따로 매스 마켓 게임이라고 부릅니다.

이 때, 저는 궁금증이 생겼습니다.

매스 마켓 게임 할 때, 매스는 수학인가? 아니면 매스는 질량인가?

아쉽게도 매스는 수학이 아닌, 질량도 아닌, "Mass=많은" 이라는 영어 단어였습니다.

그렇다면, 수학과 보드게임을 연관시킬 수는 없을까요?

절대 아닙니다.

보드게임 중에서도 수학에 관련된 보드게임이 많습니다.

그중에서도 저는 많은 분들이 쉽게 사용하셨을 법한, 그리고, 어린이들도 쉽게 즐겼을 도블 보드게임에 대해 수학과 관련해서 소개해보려고 합니다.

도블에 왜 수학원리가 사용되었는지 궁금하실 수 있습니다.

도블은, 각각 8개의 그림이 한 카드 당 있고, 각각 카드끼리 서로 같은 그림이 들어가있는 갯수는 오직 1개뿐입니다.

1개만 같은 그림이 있다니 정말 신기할 수 밖에 없습니다.

도블은 수학원리 중에서도 "파노평면 수학이론"이라는 이론을 사용했습니다.

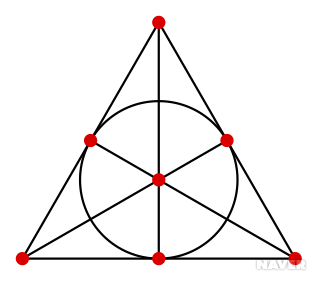
파노평면 수학이론은, 두 선이 반드시 하나의 점에서 만난다는 이론입니다.

이 게임을 만들 때, 유명한 퍼즐인 The ladie's problem을 사용했다고 합니다.

"기숙사에 있는 15명의 여학생이 3명씩 그룸을 만들어 일주일 동안 매일 산책을 나갑니다. 일주일 동안 각각의 학생은 같은 그룹에서 서로 딱 1번만 만날 수 있습니다."

정말 신기하죠!

이렇게 작고 쉬운 보드게임 속에서도 수학원리를 찾을 수 있는 만큼, 여러분들도, 작고 쉬운 보드게임을 만들더라도, 이러한 원리를 사용해보세요!

다음 번에도 그럼, 재미있는 기사 들고 올게요!

이번 기사의 퀴즈!

1. 도블에 사용된 수학이론은?

2. 도블외의 보드게임 중 수학 원리가 사용된 보드게임은?

*퀴즈의 정답은 비댓으로 달아주세요!

기사 참고: 도블 설명서

이미지 출처: (1)네이버 블로그 (2)네이버: 파노평면 수학이론 (3)도블 보드게임

대표 이미지 출처: (3)도블 보드게임

태그

#도블 #파노평면_수학이론 #코로나

A PHP Error was encountered

Severity: Warning

Message: Undefined variable $tag_news_list

Filename: inc/article_view.php

Line Number: 90

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/article_view.php
Line: 90
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Article.php
Line: 221
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: Cannot modify header information - headers already sent by (output started at /volume1/web/PhpstormProjects/www_polymath_co_kr/system/core/Exceptions.php:271)

Filename: core/Common.php

Line Number: 570

Backtrace:

An uncaught Exception was encountered

Type: TypeError

Message: count(): Argument #1 ($value) must be of type Countable|array, null given

Filename: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/article_view.php

Line Number: 90

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Article.php
Line: 221
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once